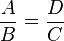1 Que debemos conocer en el problema de un trabajo de investigación
objetivos dela investigación
2 Que debe indicar el titulo del proyecto de una investigación
donde, que, como, cuando y las variables que se interrelaciona
3 Cual es la característica para definir la formulación del problema
a través de una interrogante
4 Con que verbo se debe redactar un problema de investigación
con verbos en infinitivo
5 Que pregunta se pueden formular con los objetivos de una investigación
¿Para que se busca con la investigación?
6 A que se refiere la justificación de un trabajo de investigación.
a todas las  motivaciones que llevan a investigar
7 porque es importante verificar las limitaciones de un proyecto
consegir fuentes de datos, el lugar y el espacio
8 En que consiste el marco de referencia en un proyecto
en el proceso y la realidad del entorno
9 Aquel se refiere los fundamentos teóricos en un trabajo de investigación
a la literatura que se encuentra del tema
10 A que se debe  someter la elaboración de una hipótesis
comprobación al final de la investigación

Read More

Filósofos más importantes de la historia

Filósofos más importantes de la historia

SÓCRATES:
Sócrates (c. 470-c. 399 a.C.), Fue un filósofo griego fundador de la filosofía moral, o axiología que ha tenido gran peso en la filosofía occidental por su influencia sobre Platón. Nacido en Atenas, hijo de Sofronisco, un escultor, y de Fenareta, una comadrona, recibió una educación tradicional en literatura, música y gimnasia. Más tarde, se familiarizó con la retórica y la dialéctica de los sofistas, las especulaciones de los filósofos jonios y la cultura general de la Atenas de Pericles. Al principio, Sócrates siguió el trabajo de su padre; realizó un conjunto de estatuas de las tres Gracias, que estuvieron en la entrada de la Acrópolis hasta el siglo II a.C. Durante la guerra del Peloponeso contra Esparta, sirvió como soldado de infantería con gran valor en las batallas de Potidaea en el 432-430 a.C., Delio en el 424 a.C., y Anfípolis en el 422 a.C.

TALES DE MILETO

Tales de Mileto (c. 625-c. 546 a.C.),Fue un filósofo griego nacido en Mileto (Asia Menor). Fue el fundador de la filosofía griega, y está considerado como uno de los Siete Sabios de Grecia. Tales llegó a ser famoso por sus conocimientos de astronomía después de predecir el eclipse de sol que ocurrió el 28 de mayo del 585 a.C. Se dice también que introdujo la geometría en Grecia. Según Tales, el principio original de todas las cosas es el agua, de la que todo procede y a la que todo vuelve otra vez. Antes de Tales, las explicaciones del universo eran mitológicas, y su interés por la sustancia física básica del mundo marca el nacimiento del pensamiento científico. Tales no dejó escritos; el conocimiento que se tiene de él procede de lo que se cuenta en la Metafísica de Aristóteles.

PLATÓN

Platón (c. 428-c. 347 a.C.), Fue un filósofo griego, uno de los pensadores más creativos e influyentes de la filosofía occidental.
Platón nació en el seno de una familia aristocrática en Atenas. Su padre, Aristón, era al parecer, descendiente de los primeros reyes de Atenas. Perictione, se llamaba su madre.
De joven, Platón tuvo ambiciones políticas pero se desilusionó con los gobernantes de Atenas. Más tarde se proclamó discípulo de Sócrates, aceptó su filosofía y su forma dialéctica de debate: la obtención de la verdad mediante preguntas, respuestas y más preguntas.

ARISTÓTELES

Aristóteles (384-322 a.C.),Fue un filósofo y científico griego que comparte junto a Platón y Sócrates la distinción de ser los filósofos más destacados de la antigüedad. Nacido en Estagira (Macedonia), hijo de un médico de la corte real, Aristóteles se trasladó a Atenas a los 17 años para estudiar en la Academia de Platón. Permaneció en esta ciudad unos 20 años, primero como estudiante y más tarde como maestro.

HERACLITO

Heráclito (c. 540-c. 475 a.C.aproximadamente) de Efeso en Asia Menor.
Nació en Éfeso, una antigua ciudad griega en Asia Menor, que ahora pertenece a Turquía. Debido a su vida solitaria, y a la oscuridad y misantropía de su filosofía, es llamado algunas veces el oscuro.
Fue un filósofo griego, quien sostenía que el fuego era el origen primordial de la materia y que el mundo entero se encontraba en un estado constante de cambio. El pensaba que precisamente los cambios constantes eran los rasgos mas básicos de la naturaleza.

ANAXIMENES

Anaxímenes (c. 570-500 a.C.), Fue un filósofo griego de la naturaleza, el último miembro de la escuela jónica fundada por el filósofo Tales de Mileto. Nació en Mileto (Jonia), en Asia Menor. Anaxímenes afirmaba que el aire es el elemento primario al que todas las demás cosas pueden ser reducidas.
Anaximenes conoció la teoría de Tales de Mileto ¿pero de donde viene el agua?, Anaxímenes opinaba que el agua tenia que ser aire condensado, pues vemos como el agua surge del aire cuando llueve . Y cuando el agua se condensa aun mas, se convierte en tierra.

ANAXIMANDRO

Anaximandro (c. 611-c. 547 a.C.),Fue un filósofo, matemático y astrónomo griego, que también vivió en Mileto.
Nació en Mileto (en la actual Turquía). Discípulo y amigo del filósofo griego Tales de Mileto, Anaximandro está considerado el descubridor de la oblicuidad de la eclíptica, que es el ángulo que forman el plano de la eclíptica y el plano del ecuador celeste. También se le considera introductor del reloj de sol en Grecia y fundador de la cartografía.

PITÁGORAS

Pitágoras (c. 582-c. 500 a.C.), filósofo y matemático griego, cuyas doctrinas influyeron mucho en Platón. Nacido en la isla de Samos, Pitágoras fue instruido en las enseñanzas de los primeros filósofos jonios Tales de Mileto, Anaximandro y Anaxímenes. Se dice que Pitágoras había sido condenado a exiliarse de Samos por su aversión a la tiranía de Polícrates. Hacia el 530 a.C. se instaló en Crotona, una colonia griega al sur de Italia, donde fundó un movimiento con propósitos religiosos, políticos y filosóficos, conocido como pitagorismo. La filosofía de Pitágoras se conoce sólo a través de la obra de sus discípulos.

LA EDAD MEDIA:

SAN AGUSTÍN DE HIPONA

San Agustín que vivio del 354 al 430, Fue el más grande de los padres de la Iglesia y uno de los más eminentes dores de la Iglesia occidental. Agustín nació el 13 de noviembre del año 354 en la pequeña ciudad de Tagaste,en el norte de África, Numidia (hoy Souk-Ahras, Argelia). Su padre, Patricio (fallecido hacia el año 371), era un pagano (más tarde convertido al cristianismo), pero su madre, Mónica, era una devota cristiana que dedicó toda su vida a la conversión de su hijo, siendo canonizada por la Iglesia católica romana. 

Read More

Eratóstenes

Eratóstenes era hijo de Aglaos. Estudió en Alejandría y durante algún tiempo en Atenas. Fue discípulo de Aristón de Quíos, de Lisanias de Cirene y del poeta Calímaco y también gran amigo de Arquímedes. En el año 236 a. C., Ptolomeo III le llamó para que se hiciera cargo de la Biblioteca de Alejandría, puesto que ocupó hasta el fin de sus días. La Suda afirma que, tras perder la vista, se dejó morir de hambre a la edad de 80 años; sin embargo, Luciano dice que llegó a la edad de 82 años; también Censorino sostiene que falleció cuando tenía 82 años.

Eratóstenes poseía una gran variedad de conocimientos y aptitudes para el estudio. Astrónomo, poeta, geógrafo y filósofo, su apellido fue Pentathlos, nombre que se reservaba al atleta vencedor en las cinco competiciones de los Juegos Olímpicos. Suidas afirma que también era conocido como el segundo Platón y diversos autores dicen que se le daba el sobrenombre de Beta, por la segunda letra del alfabeto griego, porque ocupó el segundo lugar en todas las ramas de la ciencia que cultivó.

 

Medición de las dimensiones de la Tierra

En el solsticio de verano, los rayos solares inciden perpendicularmente sobre Siena (Asuán). En Alejandría, más al norte, midiendo la altura de un edificio y la longitud de la sombra que proyecta, se puede determinar el ángulo formado con el plano de la eclíptica, en el que se encuentran el Sol y la ciudad de Siena, ángulo que es precisamente la diferencia de latitud entre ambas ciudades. Conocida ésta, basta medir el arco de circunferencia y extrapolar el resultado a la circunferencia completa (360º).

Reconstrucción del siglo XIX (según Bunbury) del mapa de Eratóstenes del mundo conocido en su época.

Sin embargo, el principal motivo de su celebridad es sin duda la determinación del tamaño de la Tierra. Para ello inventó y empleó un método trigonométrico, además de las nociones de latitud y longitud, al parecer ya introducidas por Dicearco, por lo que bien merece el título de padre de la geodesia.
Por referencias obtenidas de un papiro de su biblioteca, sabía que en Siena (hoy Asuán, Egipto) el día del solsticio de verano los objetos verticales no proyectaban sombra alguna y la luz alumbraba el fondo de los pozos; esto significaba que la ciudad estaba situada justamente sobre la línea del trópico y su latitud era igual a la de la eclíptica que ya conocía. Eratóstenes, suponiendo que Siena y Alejandría tenían la misma longitud (realmente distan 3º) y que el Sol se encontraba tan alejado de la Tierra que sus rayos podían suponerse paralelos, midió la sombra en Alejandría el mismo día del solsticio de verano al mediodía, demostrando que el cenit de la ciudad distaba 1/50 parte de la circunferencia, es decir, 7º 12' del de Alejandría. Según Cleomedes, Eratóstenes se sirvió del scaphium o gnomon (un protocuadrante solar) para el cálculo de dicha cantidad.
Posteriormente, tomó la distancia estimada por las caravanas que comerciaban entre ambas ciudades, aunque bien pudo obtener el dato en la propia Biblioteca de Alejandría, fijándola en 5000 estadios, de donde dedujo que la circunferencia de la Tierra era de 250.000 estadios, resultado que posteriormente elevó hasta 252000 estadios, de modo que a cada grado correspondieran 700 estadios. También se afirma que Eratóstenes, para calcular la distancia entre las dos ciudades, se valió de un regimiento de soldados que diera pasos de tamaño uniforme y los contara.
Admitiendo que Eratóstenes usase el estadio ático-italiano de 184.8 m, que era el que solía utilizarse por los griegos de Alejandría en aquella época, el error cometido sería de 6.192 kilómetros (un 15 %). Sin embargo, hay quien defiende que empleó el estadio egipcio (300 codos de 52,4 cm), en cuyo caso la circunferencia polar calculada hubiera sido de 39614 km, frente a los 40008 km considerados en la actualidad, es decir, un error de menos del 1%.
Ahora bien, es imposible que Eratóstenes diera con la medida exacta de la circunferencia de la Tierra debido a errores en los supuestos que calculó. Tuvo que haber tenido un margen de error considerable y por lo tanto no pudo haber usado el estadio egipcio: ^[2]

1. Supuso que la Tierra es perfectamente esférica, lo que no es cierto. Un grado de latitud no representa exactamente la misma distancia en todas las latitudes, sino que varía ligeramente de 110,57 km en el Ecuador hasta 111,7 km en los Polos. Por eso no podemos suponer que 7º entre Alejandría y Siena representen la misma distancia que 7º en cualquier otro lugar a lo largo de todo el meridiano.
2. Supuso que Siena y Alejandría se encontraban situadas sobre un mismo meridiano, lo cual no es así, ya que hay una diferencia de 3 grados de longitud entre ambas ciudades.
3. La distancia real entre Alejandría y Siena (hoy Asuán) no es de 924 km (5000 estadios ático-italiano de 184,8 m por estadio), sino de 843 km (distancia aérea y entre los centros de las dos ciudades), lo que representa una diferencia de 81 km.
4. Realmente Siena no está ubicada exactamente sobre el paralelo del trópico de cáncer (los puntos donde los rayos del sol caen verticalmente a la tierra en el solsticio de verano). Actualmente se encuentra situada a 72 km (desde el centro de la ciudad). Pero debido a que las variaciones del eje de la Tierra fluctúan entre 22,1 y 24,5º en un período de 41000 años, hace 2000 años se encontraba a 41 km.
5. La medida de la sombra que se proyectó sobre la vara de Eratóstenes hace 2.200 años debió ser de 7,5º o 1/48 parte de una circunferencia y no 7,2º o 1/50 parte. Puesto que en aquella época no existía el cálculo trigonométrico, para calcular el ángulo de la sombra, Eratóstenes pudo haberse valido de un compás,^[3] para medir directamente dicho ángulo, lo que no permite una medida tan precisa.

Read More

Teorema de Tales

Existen dos teoremas relacionados con la geometría clásica que reciben el nombre de teorema de Tales, ambos atribuidos al matemático griego Tales de Mileto en el siglo VI a. C.

 Los dos teoremas de Tales

El primero de ellos explica esencialmente una forma de construir un triángulo semejante a uno previamente existente ("los triángulos semejantes son los que tienen ángulos iguales y sus lados homólogos proporcionales"). Mientras que el segundo desentraña una propiedad esencial de los circuncentros de todos los triángulos rectángulos ("encontrándose éstos en el punto medio de su hipotenusa"), que a su vez en la construcción geométrica es ampliamente utilizado para imponer condiciones de construcción de ángulos rectos. Si tres o más rectas paralelas son intersecadas cada una por dos transversales, los segmentos de las transversales determinados por las paralelas, son proporcionales.

Primer teorema

Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre sí. El primer teorema de Tales recoge uno de los resultados más básicos de la geometría, a saber, que:

Teorema primero Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado. Tales de Mileto

Según parece, Tales descubrió el teorema mientras investigaba la condición de paralelismo entre dos rectas. De hecho, el primer teorema de Tales puede enunciarse como que la igualdad de los cocientes de los lados de dos triángulos no es condición suficiente de paralelismo. Sin embargo, la principal aplicación del teorema, y la razón de su fama, se deriva del establecimiento de la condición de semejanza de triángulos, a raíz de la cual se obtiene el siguiente corolario.

Corolario

Del establecimiento de la existencia de una relación de semejanza entre ambos triángulos se deduce la necesaria proporcionalidad entre sus lados. Ello significa que la razón entre la longitud de dos de ellos en un triángulo se mantiene constante en el otro.
Por ejemplo, en la figura se observan dos triángulos que, en virtud del teorema de Tales, son semejantes. Entonces, del mismo se deduce a modo de corolario que el cociente entre los lados A y B del triángulo pequeño es el mismo que el cociente entre los lados D y C en el triángulo grande. Esto es, que como por el teorema de Tales ambos triángulos son semejantes, se cumple que:

Este corolario es la base de la geometría descriptiva. Su utilidad es evidente; según Heródoto, el propio Tales empleó el corolario de su teorema para medir la altura de la pirámide de Keops en Egipto. En cualquier caso, el teorema demuestra la semejanza entre dos triángulos, no la constancia del cociente.
Del primer teorema de Tales se deduce además lo siguiente (realmente es otra variante de dicho teorema, y, a su vez, consecuencia del mismo): Si las rectas A, B, C son paralelas y cortan a otras dos rectas R y S, entonces los segmentos que determinan en ellas son proporcionales.

Segundo teorema

Ilustración del enunciado del segundo teorema de Tales de Mileto.

El segundo teorema de Tales de Mileto es un teorema de geometría particularmente enfocado a los triángulos rectángulos, las circunferencias y los ángulos inscritos, consiste en el siguiente enunciado:

Teorema segundo Sea B un punto de la circunferencia de diámetro AC, distinto de A y de C. Entonces el triángulo ABC, es un triángulo rectángulo. Tales de Mileto

Este teorema , es un caso particular de una propiedad de los puntos cocíclicos y de la aplicación de los ángulos inscritos dentro de una circunferencia.

Demostración

Siempre que AC sea un diámetro, el ángulo B será constante y recto.

 Los triángulos AOB y BOC son isósceles.

En la circunferencia de centro O y radio r (véase fig 2.3), los segmentos

OA , OB y OC

son iguales por ser todos radios de la misma circunferencia.
Por lo tanto los triángulos AOB y BOC son isósceles.
La suma de los ángulos del triángulo ABC es:

Dividiendo ambos miembros de la ecuación anterior por dos, se obtiene:

Con la expresión anterior el segundo teorema queda demostrado.

Corolarios

(Corolario 1) En todo triángulo rectángulo la longitud de la mediana correspondiente a la hipotenusa es siempre ½ de la hipotenusa.”

Ya que aplicando el teorema anterior, se sabe que para cualquier posición que adopte el vértice B vale la igualdad, OA = OB = OC = r, donde OB es la mediana de la hipotenusa.

(Corolario 2) “La circunferencia circunscripta a todo triángulo rectángulo siempre tiene radio igual a ½ de la hipotenusa y su circuncentro se ubicará en el punto medio de la misma.”

Read More

RENE DESCARTES

RENE DESCARTES  Descartes nació el 31 de marzo de 1596 en La Haye, en la Turena francesa. Pertenecía a una familia de la baja nobleza, siendo su padre, Joachin Descartes, Consejero en el Parlamento de Bretaña. La temprana muerte de su madre, Jeanne Brochard, pocos meses después de su nacimiento, le llevará a ser criado en casa de su abuela materna, a cargo de una nodriza a la que permanecerá ligado toda su vida. Posteriormente hará sus estudios en el colegio de los jesuitas de La Flèche, hasta los dieciséis años, estudiando luego Derecho en la Universidad de Poitiers. Según la propia confesión de Descartes, tanto en el Discurso del método como en las Meditaciones, las enseñanzas del colegio le decepcionaron, debido a las numerosas lagunas que presentaban los saberes recibidos, a excepción de las matemáticas, en donde veía la posibilidad de encontrar un verdadero saber. Esta muestra de escepticismo, que Descartes presenta como un rasgo personal es, sin embargo, una característica del pensamiento de finales del siglo XVI y principios del XVII, en los que el pirronismo ejerció una notable influencia. Terminados sus estudios Descartes co
mienza un período de viajes, apartándose de las aulas, convencido de no poder encontrar en ellas el verdadero saber. La noche del 10 de noviembre de 1619 tiene tres sueños sucesivos que interpreta como un mensaje del cielo para consagrarse a su misión filosófica. En 1643 conoce a Elizabeth de Bohemia, hija del elector palatino destronado y exiliado en Holanda. La princesa lo adopta como director de conciencia, de donde surgirá una abundante correspondencia en la que Descartes profundiza sobre la moral y sobre sus opiniones políticas y que le conducen en 1649 a la publicación de "Las pasiones del alma", más conocida como el Tratado de las pasiones, que será la última obra publicada en vida del autor y supervisada por él. Realiza tres viajes a Francia, en 1644, 47 y 48. Será en el curso del segundo cuando conozca a Pascal. Su fama le valdrá la atención de la reina Cristina de Suecia. Es invitado por ella en febrero de 1649 para que le introduzca en su filosofía. Descartes, reticente, parte sin embargo en septiembre para Suecia. El alejamiento, el rigor del invierno, la envidia de los doctos, contraría su estancia. La reina le cita en palacio cada mañana a las cinco de la madrugada para recibir sus lecciones. Descartes, de salud frágil y acostumbrado a permanecer escribiendo en la cama hasta media mañana, coge frío y muere de una neumonía en Estocolmo el 11 de febrero de 1650 a la edad de 53 años.

Read More

VIDEO: COMO MEDIR EL RADIO DE LA TIERRA

Read More

COMO MEDIR EL RADIO DE LA TIERRA

Calcular el radio de la Tierra a partir de la sombra de un lápiz

Los alumnos de la clase de cuarto de primaria del Colegio Ramiro de Maeztu tuvieron ayer la oportunidad de experimentar el quehacer científico y de ver que se puede hacer mucho con matemáticas muy sencillas, emulando el método que permitió al griego Eratóstenes calcular el radio de la Tierra en el 250 a. C. Eratóstenes solo necesitó medir las sombras de dos objetos verticales separados por una distancia conocida en un momento determinado del año para asegurar que la Tierra es esférica y, además, calcular sus dimensiones. En esta ocasión se calcularon las medidas a partir de la sombra de un lápiz y los datos se compartieron por videoconferencia con otros estudiantes que repetían el experimento en otro punto del mundo.

 

Como explicó David Martín de Diego, investigador del Instituto de Ciencias Matemáticas (ICMAT), en una conferencia previa al experimento, Eratóstenes obtuvo una aproximación del radio terrestre con un reducido error gracias a su ingenio, de unas sencillas observaciones y de unas matemáticas que hoy consideramos elementales.

 

Ayer fueron 75 alumnos madrileños de unos 10 años de edad, quienes asumieron el reto de averiguar el radio de la Tierra con la única ayuda de un lápiz–que proyecta su sombra en el suelo-, un porta ángulos y papel. Con ello consiguieron una de las medidas necesarias para hacer el cálculo, que luego han compartido con alumnos de otras ciudades que también participan en este proyecto internacional: Lyon (Francia) y Alejandría (Egipto),
En este experimento internacional,  total participan en torno a un millar de estudiantes. Hoy se ha celebrado en el Centro Técnico Informático del CSIC una videoconferencia en la que los alumnos de las tres ciudades han compartido y comentado sus resultados. Para conocer cuál es la longitud de la circunferencia de la Tierra es necesario saber cuál es el ángulo del Sol con respecto a la vertical en dos ciudades, así como la distancia entre éstas.
Lo que hicieron los niños del Ramiro de Maeztu fue calcular el ángulo de un triángulo rectángulo cuyos catetos son una vertical conocida –la longitud del lápiz- y su sombra.

La medición se realizó a las 14 horas 17 minutos del día 20 de junio de 2011, que es nuestro mediodía solar (12 h 17 minutos UTC) en Madrid, con una latitud de 40º 26′ Norte y una longitud de 30º 42′ oeste.
No todos los resultados se acercaron al buscado, ya que el suelo no estaba de todo nivelado, el lápiz no estaba perpendicular o a la imprecisión de las medidas tomadas. Con la ayuda de David Martin de Diego (Instituto de Ciencias Matemáticas) consiguieron una medición más precisa: 30 cm del lápiz y 9,10 cm de la sombra.
Por tanto el ángulo buscado (el que forma la dirección en la que incide el sol en la punta del palo y la vertical del palo) es el que tiene por tangente el cociente de las dos medidas:
tan a= 9,1/30=0,303
Con la calculadora han obtenido el ángulo a=16’9 grados. En Lyon deberían han medido un ángulo de 22’3 grados y en Alejandría un poco más de 8º.

Con estos datos, ya solo falta calcular las distancias en meridiano de las ciudades participantes. Por ejemplo de Madrid a Lyon hay 593 km. Sabiendo la distancia del sector de la circunferencia (593) y el valor del ángulo de este sector (22,3 – 16,9 = 5,4), haciendo una regla de tres obtenemos la longitud total del a Tierra L=39.333 km, que no es una mala estimación. Para obtener el radio de la tierra dividimos por 2xPi y nos da R=6260 km con un error del cálculo exacto de unos poco km.
La actividad fue registrada por la Fundación Española de la Ciencia y la Tecnología (FECYT). Se puede ver en el portal de la agencia de noticias científicas SINC.

Read More

DECODIFICACIÓN DE LAS FALACIAS EN UN MENSAJE

DECODIFICACIÓN DE LAS FALACIAS EN UN MENSAJE
Decodificación.- es la representación gráfica en nuestra mente al escuchar palabras conocidas, interpretando un mensaje codificado (oculto).

Es necesario analizar la información, por lo cual la DECODIFICACIÖN consiste en la interpretación de todo lo que se dice en el texto, proceso que se realiza oración por oración, poniendo atención en la información relevante.

Para decodificar las falacias en esta noticia de prensa, sigamos el siguiente proceso:

 

1.      Leamos todo el texto, luego parte por parte, señalando la información importante.

2.      Analicemos cada una de las inferencias.

3.      Utilicemos el razonamiento deductivo para obtener conclusiones a partir de una o varias premisas.

4.  Tener cuidado al construir las premisas para no caer en errores de razonamiento (falacias en el razonamiento deductivo).

 

 

 

Decodificación.- es la representación gráfica en nuestra mente al escuchar palabras conocidas, interpretando un mensaje codificado (oculto).

Maldonado (2014:27), nos dice que “ciertos anuncios publicitarios contienen una gran cantidad de falacias, es decir, errores intencionados para, en este caso vender un producto.”

Read More

Clasificacion de las falacias

Clasificación de las falacias

• A. FALACIAS FORMALES

Las falacias formales son razonamientos no válidos pero que a menudo se aceptan por su semejanza con formas válidas de razonamiento o inferencia. Se da un error que pasa inadvertido.

• 1. AFIRMACIÓN DEL CONSECUENTE

Llamado también como la confirmación sistemática, es el equivalente lógico a asumir la verdad necesaria de que lo contrario también lo es. Es llamada así porque erróneamente se concluye que el segundo término de una premisa consecuente establece también la verdad de su antecesora. Si se demuestra que P entonces Q, entonces erróneamente se puede deducir que si Q entonces P llevándonos a esta falacia, que se apoya en el sesgo de simetría.
Ejemplo: si estoy dormido tengo los ojos cerrados, entonces si tengo los ojos cerrados debo estar dormido.
Ejemplo: Si llueve, cojo el paraguas; cojo el paraguas. Entonces, llueve.

• 2. NEGACIÓN DEL ANTECEDENTE

Es una falacia lógica con semejanzas con el argumento de la falacia. En este caso si P entonces Q si niego P entonces tampoco Q (se niega Q). Esta falacia dice que si se niegan los antecedentes entonces se negará también la consecuencia.
Ejemplo: Si estoy dormido tengo los ojos cerrados, pero si estoy despierto tengo que estar con los ojos abiertos.
Ejemplo: Si llueve, cojo el paraguas; no llueve. Entonces, no cojo el paraguas

• 3. SILOGISMO DISYUNTIVO FALAZ

Razonamiento que partiendo de una disyunción y, como segunda premisa, se afirma uno de los dos componentes de la disyunción, se concluye la negación del otro componente.
Ejemplo: Te gusta la música o te gusta la lectura; te gusta la música. Entonces no te gusta la lectura.

• B. FALACIAS INFORMALES

Las falacias no formales son razonamientos en los cuales lo que aportan las premisas no es adecuado para justificar la conclusión a la que se quiere llegar. Se quiere convencer no aportando buenas razones sino apelando a elementos no pertinentes o, incluso, irracionales. Cuando las premisas son informaciones acertadas, lo son, en todo caso, por una conclusión diferente a la que se pretende.

• 1. FALACIA AD HOMINEM (DIRIGIDO CONTRA EL HOMBRE)

Razonamiento que, en vez de presentar razones adecuadas para rebatir una determinada posición o conclusión, se ataca o desacredita la persona que la defiende.es un ataque al que argumenta y no al argumento.
Ejemplo: "Los ecologistas dicen que consumimos demasiado energía; pero no hagas caso porque los ecologistas siempre exageran".

Read More

Origen del Conocimiento

Read More

la experiencia como productora del Conocimiento

Read More

La Falacia el Error y el Acierto

Falacia

·         En lógica, una falacia es un argumento que parece válido, pero no lo es. Algunas falacias se cometen intencionalmente para persuadir o manipular a los demás, mientras que otras se cometen sin intención debido a descuidos o ignorancia.

·         En ocasiones las falacias pueden ser muy sutiles y persuasivas, por lo que se debe poner mucha atención para detectarlas.

·         El que un argumento sea falaz no implica que sus premisas o su conclusión sean falsas ni que sean verdaderas.

Error

El Error, en filosofía, es un concepto que pertenece a la esfera del juicio, es decir, de las actitudes valorativas. En general, se denomina error a todo juicio o valoración que contraviene el criterio que se reconoce como válido, en el campo al que se refiere el juicio.
Error o erróneo, en lo coloquial, puede referirse a distintos conceptos en diversos campos de conocimiento:

• Psicología y planificación:
• Error de concepto: inexactitud o equivocación al producir en la mente una idea sobre algo.
• Error de apreciación: es una inexactitud o equivocación al percibir con los sentidos y la mente un determinado fenómeno o evaluar determinada situación o problema.
• Error humano: una expresión que indica que un suceso desfavorable está fuertemente condicionado por la actividad de las personas que participan directa o indirectamente en su realización y control.

Acierto:

1   Elección de la solución correcta entre varias posibilidades: tengo doce aciertos en la quiniela.

2   Acción que tiene éxito u obtiene el resultado adecuado: ha sido un acierto salir a cenar esta noche.

3   Habilidad al hacer una cosa: tiró al blanco con gran acierto.

Read More

Las Bases del Conocimiento

Read More

PENSAMIENTO RACIONAL

PENSAMIENTO RACIONAL

Este tipo de pensamiento es contrario al anterior, se basa en la lógica y el razonamiento de las cosas y situaciones, analizando las consecuencias y buscando siempre que sean las adecuadas, ayudando así al individuo a que su comportamiento sea el correcto de acuerdo a su entorno; y motivando el autoestima y la felicidad humana, mediante el cálculo razonable de las probabilidades siempre con optimismo. 

Así, pensamientos razonables podrían ser:

Debemos ser competentes y perfectos en nuestros estudios para ser alguien en la vida.

• Siempre será bueno tener alguien con quien compartir mis problemas y dificultades, para que me ayude a superarlas.
• Es más fácil evitar las dificultades e irresponsabilidades en el cumplimiento de mis tareas, que luego enfrentarlas.
• Nunca digas “no puedo”, somos capaces de hacer cosas que ni siquiera nos las imaginamos.

 

PENSAMIENTO IRRACIONAL.

 
Los pensamientos irracionales son parte de los valores que cada persona lleva arraigados como identidad, estos pensamientos casi nunca llevan lógica o algo bueno u optimista, en cambio, son mayormente negativos y afectan a la persona, sus decisiones y, por tanto, las consecuencias que estas tendrán. Basadas en creencias negativas o sin sentido, pueden ser pensamientos como:

 Ejemplos:

       "No sirvo para nada" ; "Los demás no me respetan" ; " Nunca podré superarme".

        "No puedo confiar en nadie" ; "Todos buscan dañarme"

                                          "La vida no tiene sentido" ; "Este mundo no sirve de nada..."

Estos pensamientos son auto-destructivos y sin uso de razonamiento alguno, por lo que no puede aportar nada bueno al que los posee.

Read More

ORIGEN DEL CONOCIMIENTO

El Racionalismo.

Plantea que el origen del conocimiento está en la razón, la cual es considerada como la fuente principal de éste, tal circunstancia determinada que esta posición sea considerada como exclusiva.
El racionalismo se identifica ante todo con la tradición que proviene del filósofo y científico francés del siglo XVII René Descartes, quien decía que la geometría representaba el ideal de todas las ciencias y también de la filosofía. Descartes aseguraba que solo por medio de la razón se podían descubrir ciertas verdades universales. A partir de aquellas verdades es posible deducir el resto de contenidos de la filosofía y de las ciencias. Manifestaba que estas verdades evidentes en sí eran innatas, no derivadas de la experiencia. Este tipo de racionalismo fue desarrollado por otros filósofos europeos, como el holandés Baruch Spinoza y el pensador y matemático alemán Gottfried Wilhelm Leibniz. Se opusieron a ella los empiristas británicos, como John Locke y David Hume, que creían que todas las ideas procedían de los sentidos.
El racionalismo sostiene que la fuente de conocimiento es la razón y rechaza la idea de los sentidos, ya que nos pueden engañar; defiende las ciencias exactas, en concreto las matemáticas, y dice que posee contenidos innatos, es decir, ya nacemos con conocimientos, solo tenemos que «acordarnos» de ellos. Usa el método deductivo como principal herramienta para llegar al verdadero conocimiento.
El racionalismo epistemológico ha sido aplicado a otros campos de la investigación filosófica. El racionalismo en ética es la afirmación de que ciertas ideas morales primarias son innatas en la especie humana y que tales principios morales son evidentes en sí a la facultad racional. El racionalismo en la filosofía de la religión afirma que los principios fundamentales de la religión son innatos o evidentes en sí y que la revelación no es necesaria, como en el deísmo. Desde finales del siglo XIX, el racionalismo ha jugado un papel antirreligioso en la teología.

El Empirismo.

Considera que el origen está en la experiencia. Parte de los hechos concretos y es una posición cuyo origen se encuentra fundamentalmente en las ciencias naturales.

Intelectualidad.

Es una posición entre el racionalismo y el empirismo la cual considera el conocimiento como producto de la razón y la experiencia.

El Apriorismo.

Al igual que intelectualidad, es también una posición intermedia entre el racionalismo y el empirismo ya que considera la razón y a la experiencia frente del conocimiento.
El empirismo, bajo ese nombre, surge en la Edad Moderna como fruto maduro de una tendencia filosófica que se desarrolla sobre todo en el Reino Unido desde la Baja Edad Media. Suele considerarse en contraposición al llamado racionalismo, más característico de la filosofía continental. Hoy en día la oposición empirismo-racionalismo, como la distinción analítico-sintético, no suele entenderse de un modo tajante, como lo fue en tiempos anteriores, y más bien una u otra postura obedece a cuestiones metodológicas y heurísticas o de actitudes vitales más que a principios filosóficos fundamentales. Respecto del problema de los universales, los empiristas suelen simpatizar y continuar con la crítica nominalista iniciada en la Baja Edad Media.
En la Antigüedad clásica, lo empírico se refería al conocimiento que los médicos, arquitectos, artistas y artesanos en general obtenían a través de su experiencia dirigida hacia lo útil y técnico, en contraposición al conocimiento teórico concebido como contemplación de la verdad al margen de cualquier utilidad.

Read More

Que es el Conocimiento

* Que es el Conocimiento

El conocimiento es una capacidad humana y no una propiedad de un objeto como pueda ser un libro. Su transmisión implica un proceso intelectual de enseñanza y aprendizaje. Transmitir una información es fácil, mucho más que transmitir conocimiento. Esto implica que cuando hablamos de gestionar conocimiento, queremos decir que ayudamos a personas a realizar esa actividad.

* El conocimiento carece de valor si permanece estático. Sólo genera valor en la medida en que se mueve, es decir, cuando es transmitido o transformado.

* El conocimiento genera conocimiento mediante el uso de la capacidad de razonamiento o inferencia (tanto por parte de humanos como de máquinas).

* El conocimiento tiene estructura y es elaborado, implica la existencia de redes de ricas relaciones semánticas entre entidades abstractas o materiales. Una simple base de datos, por muchos registros que contenga, no constituye per se conocimiento.

* El conocimiento es siempre esclavo de un contexto en la medida en que en el mundo real difícilmente puede existir completamente autocontenido. Así, para su transmisión es necesario que el emisor (maestro) conozca el contexto o modelo del mundo del receptor (aprendiz).

* El conocimiento puede ser explícito (cuando se puede recoger, manipular y transferir con facilidad) o tácito. Este es el caso del conocimiento heurístico resultado de la experiencia acumulada por individuos.

* El conocimiento puede estar formalizado en diversos grados, pudiendo ser también informal. La mayor parte del conocimiento transferido verbalmente es informal.

En este punto, daremos una definición táctica de conocimiento:

Conocimiento es la capacidad para convertir datos e información en acciones efectivas.

 

Read More

El Racionalismo y Empirismo

Read More